Enhancing Mathematical Capabilities in RAG PDF Applications

Math in PDFs is a mess. 

Not because it’s unreadable to humans — but because most Retrieval-Augmented Generation (RAG) systems still can’t make sense of it. They flatten logic into plain text, lose structure, and miss relationships that define what the math actually means.

That’s the real problem behind enhancing mathematical capabilities in RAG PDF applications.

It’s not about recognizing symbols — it’s about understanding how they relate, stack, nest, and build meaning through structure. 

A missed superscript or broken fraction isn’t just a formatting error; it changes the entire equation. And when RAG models rely on broken input, their outputs break too.

Enhancing mathematical capabilities in RAG PDF applications means solving this at the source: parsing, representing, and retrieving math the way it was written — structurally, semantically, and spatially. 

Let’s unpack what’s getting in the way and what’s starting to work.

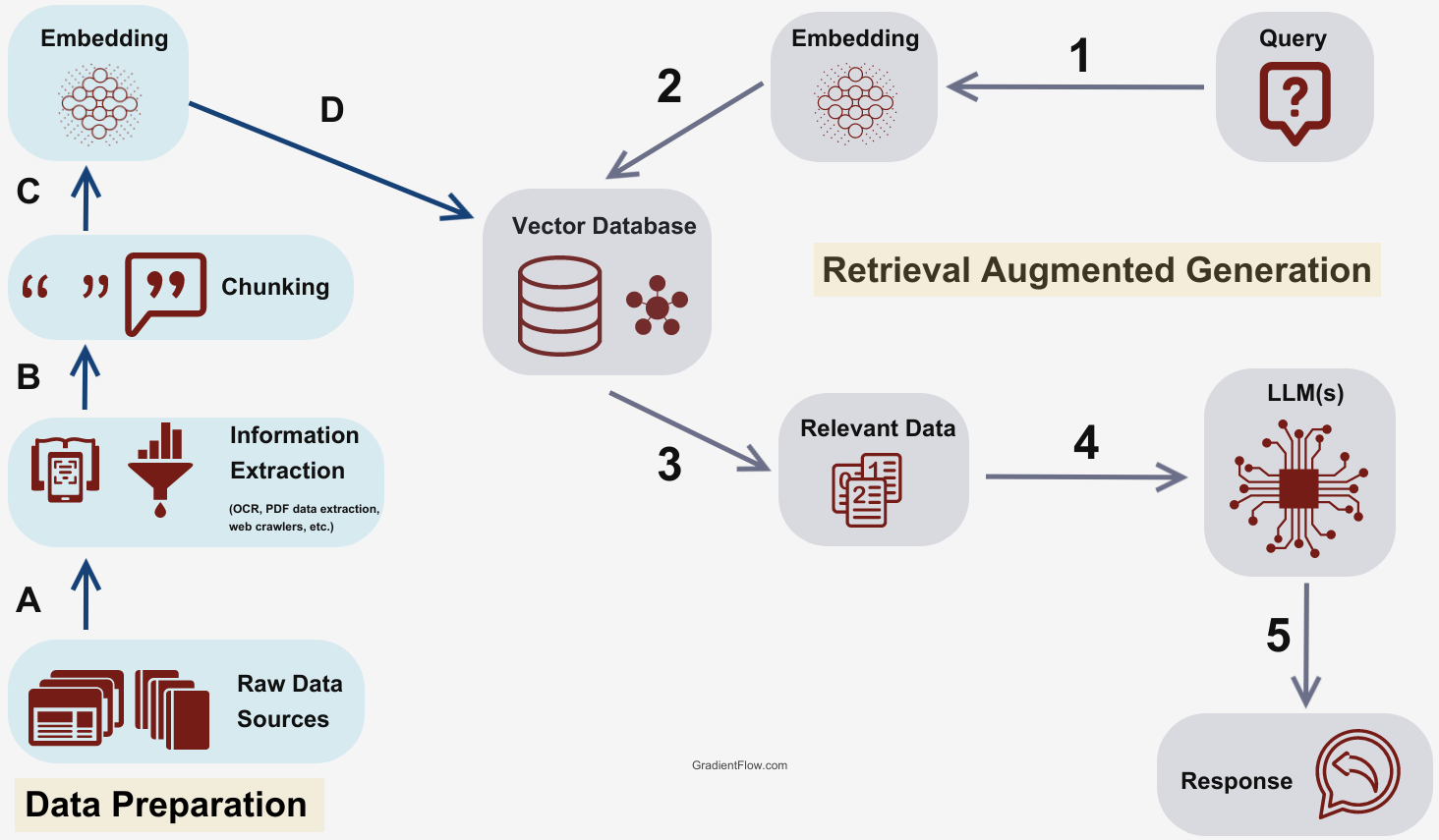
The Role of RAG in Information Retrieval

Retrieval-Augmented Generation (RAG) systems excel in handling mathematical PDFs by addressing a critical challenge: preserving the structural integrity of mathematical expressions during retrieval. 

Unlike traditional search methods, which often reduce content to plain text, RAG integrates retrieval with generative capabilities to maintain the spatial and logical relationships inherent in mathematical data.

This capability is rooted in graph-based models, where symbols are treated as nodes and their relationships as edges. 

Such models preserve the hierarchy and dependencies within equations, enabling accurate interpretation. 

For instance, when parsing a complex formula, RAG systems can retrieve the textual representation and the embedded logical structure, ensuring that the retrieved content remains semantically meaningful.

A notable implementation of this approach is seen in educational platforms that utilize RAG to generate context-aware responses to student queries.

By leveraging iterative retrieval-generation cycles, these systems adapt dynamically to the nuances of mathematical content, outperforming static retrieval methods. 

This nuanced handling of structure and context positions RAG as a cornerstone for advancing mathematical information retrieval.

Challenges in Handling Mathematical Content

Capturing the spatial hierarchy of mathematical expressions is one of the most intricate challenges in RAG systems. 

Unlike plain text, mathematical content relies on precise spatial relationships—superscripts, subscripts, and nested structures—to convey meaning. 

Misinterpreting these relationships can distort an equation's logic, rendering it unusable.

This complexity arises from the limitations of traditional OCR systems, which often fail to preserve the spatial logic embedded in mathematical layouts. 

To address this, advanced graph-based models have been developed, where symbols are treated as nodes and their spatial relationships as edges. 

These models excel in maintaining structural fidelity but demand significant computational resources, especially when handling dense or overlapping notations.

A notable example is the integration of graph-based parsing in educational platforms like Khan Academy, which ensures that retrieved mathematical content aligns with its original semantic structure. 

However, even these systems face edge cases, such as ambiguous glyphs or unconventional notations requiring manual intervention or adaptive algorithms.

Ultimately, RAG's success in mathematical contexts hinges on balancing computational efficiency with the need for structural accuracy, a trade-off that continues to shape its evolution.

Parsing Mathematical PDFs

Parsing mathematical PDFs is akin to solving a multidimensional puzzle where every piece—symbols, spatial relationships, and logical hierarchies—must align perfectly. 

A standout challenge lies in decoding multi-line equations, where even a slight misalignment in baselines can disrupt semantic coherence. 

For instance, a misplaced fraction bar can invert the meaning of an entire formula, rendering it useless for downstream RAG applications. 

This underscores the necessity of precision in every parsing step.

One effective approach involves leveraging stochastic context-free grammars, which dynamically adapt to diverse document structures. 

Unlike static OCR systems, these algorithms normalize font encoding and symbol placement inconsistencies, ensuring robust parsing even in edge cases. 

For example, Neo4j’s graph-based models preserve nested hierarchies by treating symbols as nodes and their relationships as edges, enabling seamless integration into RAG pipelines.

Consider this process translating a symphony into sheet music: every note (symbol) and its position (spatial relationship) must be captured to preserve the original intent. 

Practitioners unlock unparalleled accuracy by embedding parsed outputs into structured formats like LaTeX or JSON, transforming raw data into actionable intelligence.

Techniques for Accurate PDF Parsing

Parsing mathematical PDFs demands a nuanced approach, especially when dealing with multi-layered content. 

One standout technique is Tree-based Parsing, which constructs hierarchical expression trees to represent the logical structure of formulas. 

This method breaks down equations into discrete components—operators, operands, and groupings—while preserving their spatial and semantic relationships.

What sets Tree-based Parsing apart is its ability to handle nested hierarchies, such as fractions within radicals or superscripts tied to specific variables. 

Mapping these relationships explicitly ensures that even the most complex expressions retain their logical coherence. 

However, its effectiveness hinges on robust layout analysis to identify spatial cues like alignment and spacing, which are critical for accurate tree construction.

A comparative analysis reveals that while OCR-based systems often misinterpret stacked or ambiguous notations, tree-based models maintain clarity by explicitly modeling relationships. 

For instance, the Zanibbi Group’s Tangent Search Engine leverages Symbol Layout Trees (SLTs) to achieve high-precision retrieval, outperforming traditional parsers in both accuracy and scalability.

By embedding these trees into structured formats like MathML, practitioners unlock seamless integration with RAG systems, transforming static PDFs into dynamic, machine-readable assets. 

This approach enhances retrieval accuracy and sets a new standard for mathematical content parsing.

Overcoming Spatial and Semantic Challenges

Accurately parsing mathematical PDFs requires addressing the intricate interplay between spatial positioning and semantic meaning. 

A particularly effective technique involves Line-of-Sight (LOS) graphs, which connect symbols only when visually unobstructed. 

This approach ensures that spatial relationships, such as the alignment of superscripts or nested radicals, are preserved during parsing.

LOS graphs stand out because they can handle edge cases like overlapping symbols or detached components, which often confuse traditional OCR systems. 

By indexing symbols based on their relative positions and size ratios, LOS graphs accurately reconstruct even the most complex expressions. 

However, their effectiveness depends on robust preprocessing to normalize font encoding and document formatting inconsistencies.

A notable implementation of this method was seen in the NTCIR-12 Wikipedia Formula Browsing Task, where LOS graphs significantly improved formula indexing accuracy. 

Yet, challenges persist, particularly with ambiguous notations that require adaptive algorithms for disambiguation.

By integrating LOS graphs into RAG pipelines, practitioners can bridge the gap between raw parsing and structured representation, ensuring that even subtle spatial nuances are faithfully encoded. 

This meticulous attention to detail transforms static PDFs into actionable, machine-readable assets.

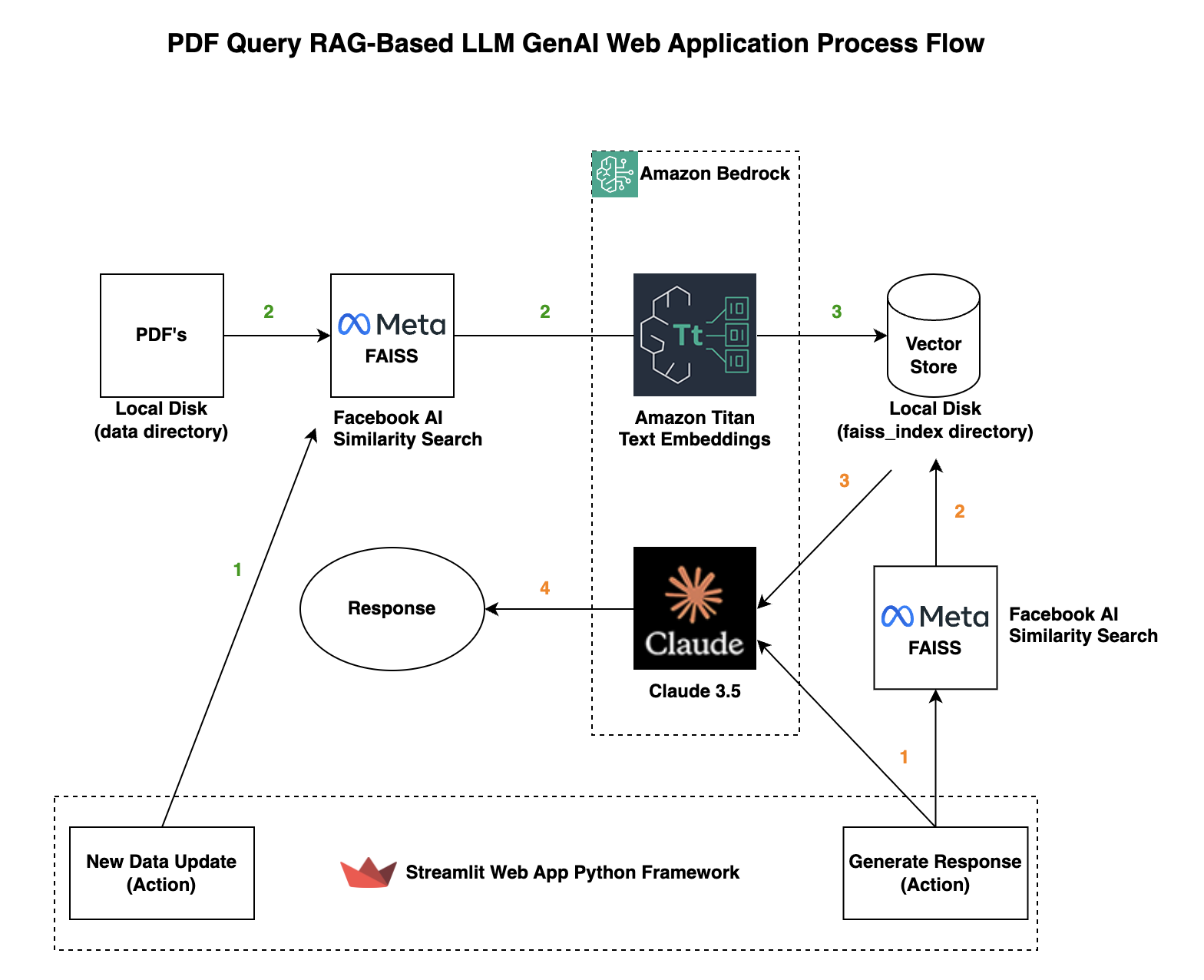
Structured Data Representation

Structured data representation is the cornerstone of transforming mathematical PDFs into actionable assets for Retrieval-Augmented Generation (RAG) systems. 

Unlike plain text, mathematical content encodes meaning through spatial hierarchies and logical dependencies, which must be meticulously preserved. 

A pivotal breakthrough lies in graph-based data models, where symbols are treated as nodes and their relationships as edges. 

This approach ensures that nested structures, such as matrices or radicals, retain their semantic integrity, enabling precise downstream computations.

A common misconception is that static formats like LaTeX inherently preserve structure. However, without normalization techniques to address inconsistencies in font encoding or ambiguous notations, even LaTeX outputs can fail. 

By embedding iterative validation into RAG pipelines, practitioners ensure that every parsed formula aligns with its original intent, bridging the gap between raw data and intelligent retrieval.

Converting Mathematical Content to LaTeX and JSON

Converting mathematical content into LaTeX and JSON requires a meticulous approach to preserve spatial and semantic integrity. 

A critical challenge lies in mapping nested hierarchies, such as radicals within fractions, into machine-readable formats without losing their contextual meaning. 

This process demands spatial analysis and semantic tagging to ensure that every symbol’s role and relationship are accurately represented.

One effective methodology involves integrating adaptive normalization algorithms during the conversion process. 

These algorithms dynamically adjust for font encoding and symbol alignment inconsistencies, common in mathematical PDFs. 

For instance, normalization ensures that their relative positions are preserved when handling superscripts or subscripts, preventing logical errors in the output.

A comparative analysis reveals that while LaTeX excels in academic contexts for its precision, JSON offers unparalleled flexibility for integrating RAG systems. 

JSON’s hierarchical structure mirrors the spatial dependencies captured during parsing, making it ideal for downstream applications like automated theorem proving.

Ultimately, the success of this conversion hinges on balancing automation with manual validation. 

By embedding iterative checks into the pipeline, practitioners can ensure that the output faithfully reflects the original document’s complexity, enabling seamless integration into advanced RAG workflows.

Graph-Based Models for Mathematical Expressions

Graph-based models capture the intricate spatial and logical relationships within mathematical expressions, transforming them into structured, machine-readable formats. 

These models preserve the hierarchy and dependencies that define mathematical meaning by treating each symbol as a node and its relationships as edges. 

This approach is particularly effective for nested structures, such as radicals within fractions, where traditional methods often falter.

The strength of graph-based models lies in their ability to encode both spatial positioning and semantic roles simultaneously. 

For example, these models maintain continuity across lines by mapping relationships beyond visual boundaries when parsing a multi-line equation. 

This ensures that the formula's logical flow remains intact, even in complex layouts. However, their computational intensity and reliance on robust preprocessing pipelines present challenges, especially when handling ambiguous notations or overlapping symbols.

A notable implementation of this technique is seen in academic publishing workflows, where tools like Neo4j integrate graph-based representations to enhance retrieval accuracy.

These systems achieve unparalleled precision in querying and reasoning tasks by embedding parsed formulas into graph databases.

One emerging insight is the adaptability of these models across diverse contexts, from automated theorem proving to domain-specific question answering. 

By iteratively refining graph structures, practitioners can bridge the gap between raw mathematical data and actionable intelligence, setting a new standard for RAG applications.

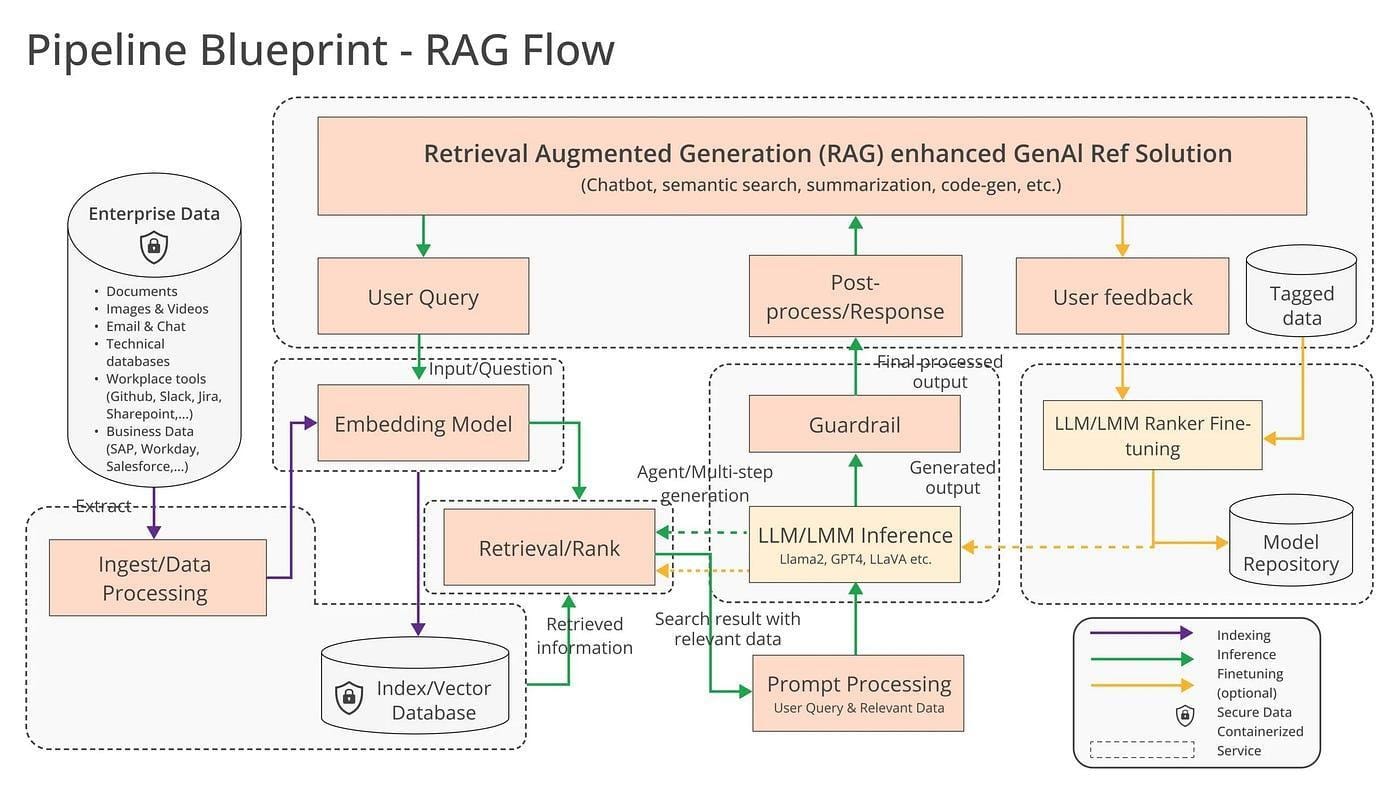
Integrating Parsed Data into RAG Pipelines

Integrating parsed mathematical data into Retrieval-Augmented Generation (RAG) pipelines demands precision and adaptability. 

A critical insight is that raw parsed outputs, such as LaTeX or MathML, often require normalization to resolve inconsistencies in font encoding or ambiguous notations. 

Without this step, even advanced RAG systems risk misinterpreting nested structures like matrices or radicals, leading to flawed outputs.

One transformative approach involves embedding graph-based representations into RAG workflows. 

Think of this process as translating a symphony into a digital score: every note (symbol) and its timing (spatial relationship) must align perfectly. 

By iteratively refining these representations, practitioners unlock scalable, high-fidelity mathematical reasoning, setting a new benchmark for RAG applications.

Enhancing RAG Systems with Structured Data

Graph-based representations are a cornerstone for enhancing RAG systems, mainly when dealing with mathematical data. 

These models preserve the spatial and semantic hierarchies that define mathematical meaning by treating symbols as nodes and their relationships as edges. 

This approach ensures that nested structures, such as radicals within fractions, are encoded precisely, enabling accurate downstream computations.

A critical mechanism here is the iterative validation process. Unlike static parsing methods, graph-based models dynamically adapt to edge cases, such as overlapping glyphs or ambiguous notations. 

This adaptability is particularly valuable in contexts where PDFs lack consistent encoding standards, as it bridges gaps left by traditional OCR systems. 

For example, Neo4j’s integration of graph-based data into RAG workflows has significantly improved retrieval accuracy by maintaining structural fidelity.

However, this technique is not without challenges. 

Computational intensity and the need for robust preprocessing pipelines can limit scalability. Yet, when implemented effectively, graph-based models transform raw mathematical data into actionable intelligence, setting a new standard for RAG applications.

Iterative and Recursive Retrieval Techniques

Iterative and recursive retrieval techniques in RAG pipelines function as a dynamic refinement process, ensuring that every layer of mathematical complexity is accurately captured. 

Unlike static retrieval, which risks overlooking nuanced relationships, these methods revisit and refine data extraction, adapting to the intricacies of mathematical content.

The core mechanism involves breaking down formulas into their fundamental components and iteratively validating their spatial and semantic relationships. 

Recursive retrieval extends this by re-querying based on intermediate results, enabling the system to resolve ambiguities or inconsistencies. 

For example, recursive steps ensure continuity across lines when parsing a multi-line equation, preserving the logical flow that static methods often disrupt.

A notable implementation of this approach is seen in Neo4j’s graph-based RAG workflows, where iterative validation significantly enhances retrieval accuracy. 

By embedding parsed data into graph structures, these systems dynamically adapt to edge cases, such as overlapping symbols or unconventional notations, ensuring structural fidelity.

One unexpected challenge lies in balancing computational efficiency with the depth of recursion. 

Excessive iterations can strain resources, particularly with dense or poorly formatted PDFs. 

However, adaptive algorithms that prioritize high-impact refinements mitigate this issue, making iterative and recursive retrieval indispensable for handling the layered complexity of mathematical data.

This approach transforms static parsing into a dynamic, context-aware process, unlocking new possibilities for RAG applications.

FAQ

Conclusion

Enhancing mathematical capabilities in RAG PDF applications depends on preserving mathematical content's spatial and logical structures. 

Graph-based models, adaptive normalization, and semantic tagging form the core of accurate parsing and structured representation. 

These methods ensure that formulas retain their meaning across retrieval and generation. As real-world use cases in legal, academic, and technical domains grow, structured mathematical parsing will continue to play a key role in how RAG systems process complex PDFs.