Parsing Mathematical PDFs for Enhanced RAG Applications

Most AI systems struggle when faced with one thing: math in PDFs. 

Parsing Mathematical PDFs for Enhanced RAG Applications is harder than it looks. 

Unlike plain text, formulas don’t follow a simple left-to-right order. 

Their meaning depends on spatial layout — superscripts, fractions, nested symbols. Miss one detail, and you lose the logic.

The problem isn’t just technical. In Retrieval-Augmented Generation (RAG) systems, even a single misread symbol can break downstream reasoning. A misplaced exponent or misaligned matrix turns useful knowledge into noise. 

That’s why parsing mathematical PDFs for enhanced RAG applications isn’t a nice-to-have — it’s the foundation for accuracy in scientific, legal, and technical domains.

This article walks through the structural complexity behind mathematical PDFs, breaks down what makes them hard to parse, and explores the tools and techniques that help RAG systems extract them accurately, down to the smallest index.

Fundamentals of PDF Structure

PDFs are not linear documents; they are hierarchical constructs where every element—text, images, and glyphs—is encapsulated in discrete objects. 

At the core of this structure lies the content stream, a sequence of instructions that define how each element is rendered on the page. 

Parsing tools must navigate this intricate hierarchy, decoding the visible content and the spatial and logical relationships embedded within.

One critical challenge is the layered nature of PDFs. Unlike traditional documents, PDFs often overlay elements, such as mathematical symbols and annotations, in separate layers. 

This layering can obscure the semantic connections between components, particularly in mathematical formulas where spatial positioning conveys meaning. 

For instance, superscripts and subscripts rely on precise vertical alignment, which many parsers fail to interpret accurately.

A comparative analysis of parsing methodologies reveals that rule-based systems excel in extracting structured data from predictable layouts but falter with complex, multi-layered documents. 

Conversely, machine learning models, such as those leveraging graph-based representations, demonstrate superior adaptability but require extensive training data and computational resources.

By combining layout analysis with meaning, advanced parsers turn raw math data into useful information, making it easier for systems like RAG to understand and use.

Text Extraction Techniques

Extracting text from PDFs, particularly mathematical content, hinges on decoding the spatial and logical relationships embedded within the document’s structure. 

A standout technique involves leveraging font metadata and glyph bounding boxes to reconstruct text elements' geometric and semantic context. This approach surpasses traditional OCR by directly accessing the PDF’s internal data, preserving nuances like superscript alignment or fraction positioning.

One critical advantage of this method is its ability to handle multi-layered content. For example, mathematical expressions often include overlapping elements, such as annotations or nested radicals, which can confuse simpler extraction tools. 

By analyzing the precise spatial coordinates of each glyph, advanced parsers can maintain the integrity of these relationships, ensuring accurate representation.

However, this technique is not without challenges. 

Variations in font encoding across PDFs can lead to inconsistencies, requiring adaptive algorithms to normalize data. Additionally, edge cases, such as underspecified matrix representations, demand specialized handling to avoid semantic loss.

By integrating these principles with machine learning for anomaly detection, parsers can achieve unparalleled accuracy, bridging the gap between raw data and meaningful interpretation.

Techniques for Mathematical Content Extraction

Another effective technique for mathematical content extraction is Tree-based Parsing, which builds expression trees to represent the hierarchical structure of mathematical formulas. 

This method breaks down equations into components like operators, operands, and groupings, capturing the syntax in a way that reflects how humans read and solve them.

A notable implementation is seen in the Zanibbi Group’s Tangent Search Engine, which parses mathematical expressions into Symbol Layout Trees (SLTs). 

These trees preserve spatial relationships, such as baseline shifts in fractions or nesting in radicals, allowing precise search and retrieval from large mathematical corpora.

Tree-based parsing supports better alignment between visual representation and logical meaning, especially when combined with layout-aware models. 

Unlike flat token sequences, these trees reflect the recursive nature of math, capturing depth and grouping. This is essential for RAG systems that rely on clear and structured inputs to generate accurate responses.

While traditional parsers may misread stacked or ambiguous notation, tree-based approaches maintain clarity by modeling relationships explicitly. 

This structure enables high-precision retrieval, making it an ideal technique for powering math-aware Retrieval-Augmented Generation pipelines.

Image source: youtube.com

Recognizing Mathematical Symbols

Parsing mathematical symbols from PDFs requires a nuanced understanding of their spatial and contextual relationships. 

Unlike plain text, symbols often derive meaning from their precise positioning—superscripts, subscripts, and nested structures all depend on relative alignment. 

This complexity makes traditional OCR systems inadequate, as they frequently misinterpret overlapping or closely spaced glyphs.

One advanced approach involves leveraging Line-of-Sight (LOS) graphs, which connect symbols only when they are visually unobstructed. 

This method, as applied in the NTCIR-12 Wikipedia Formula Browsing Task, ensures that spatial relationships are preserved during parsing. 

By indexing symbols based on their relative positions and size ratios, LOS graphs enable accurate reconstruction of even intricate mathematical expressions.

However, challenges persist. 

Variations in font encoding and document formatting can disrupt symbol recognition, particularly in edge cases like compound glyphs or ambiguous notations. 

For instance, root symbols with detached components often require specialized handling to avoid semantic errors.

Hybrid systems combining LOS graphs with machine learning models have emerged to address these issues.

These systems adapt dynamically to diverse document structures, offering a robust solution for applications like Retrieval-Augmented Generation. 

By integrating geometric precision with adaptive algorithms, they bridge the gap between theoretical parsing and practical implementation.

Converting Mathematical Notations to LaTeX

Converting mathematical notations to LaTeX requires more than just recognizing symbols; it demands understanding the spatial and semantic interplay that defines mathematical expressions. 

A critical aspect often overlooked is the alignment of glyphs, which encodes relationships like superscripts, subscripts, and fractions. 

These spatial cues are essential for generating accurate LaTeX representations.

One effective methodology involves combining spatial analysis with semantic categorization. 

By mapping glyph positions relative to one another, systems can infer hierarchical structures, such as nested radicals or matrix layouts. 

This approach surpasses traditional OCR by preserving the integrity of two-dimensional arrangements, ensuring that the resulting LaTeX code reflects the original expression’s intent.

A comparative analysis reveals that while OCR-based systems struggle with ambiguous layouts, tools leveraging PDF metadata—such as font sizes and bounding boxes—excel in maintaining structural fidelity. 

However, these systems face challenges when PDFs lack consistent encoding standards, leading to errors in symbol interpretation.

An emerging solution is the integration of machine learning models trained on annotated datasets. 

These models dynamically adapt to diverse document formats, bridging gaps left by static algorithms. This hybrid approach enhances accuracy and sets a foundation for seamless integration into Retrieval-Augmented Generation workflows.

Structured Data Representation for RAG Systems

Structured data representation is the linchpin of effective Retrieval-Augmented Generation (RAG) systems, particularly when dealing with mathematical PDFs. 

Even the most advanced AI models falter in interpreting complex formulas without a precise framework. The challenge lies in encoding mathematical content's spatial and semantic intricacies into machine-readable formats like JSON or LaTeX.

A pivotal technique involves leveraging graph-based data models to preserve hierarchical relationships. 

For instance, nested radicals or superscripts are mapped as nodes and edges, ensuring their spatial dependencies remain intact. 

As demonstrated by the MIaS system, this approach enables integration of over 112 million formulas into searchable databases, highlighting its scalability and precision.

Misconceptions often arise around the sufficiency of OCR for such tasks. While OCR captures visual elements, it fails to encode logical structures, leading to semantic errors. 

By contrast, hybrid systems combining layout analysis with semantic tagging ensure that every symbol’s role—operator, variable, or constant—is accurately represented.

This meticulous structuring enhances RAG system accuracy and unlocks new possibilities for AI-driven research, from automated theorem proving to advanced scientific discovery.

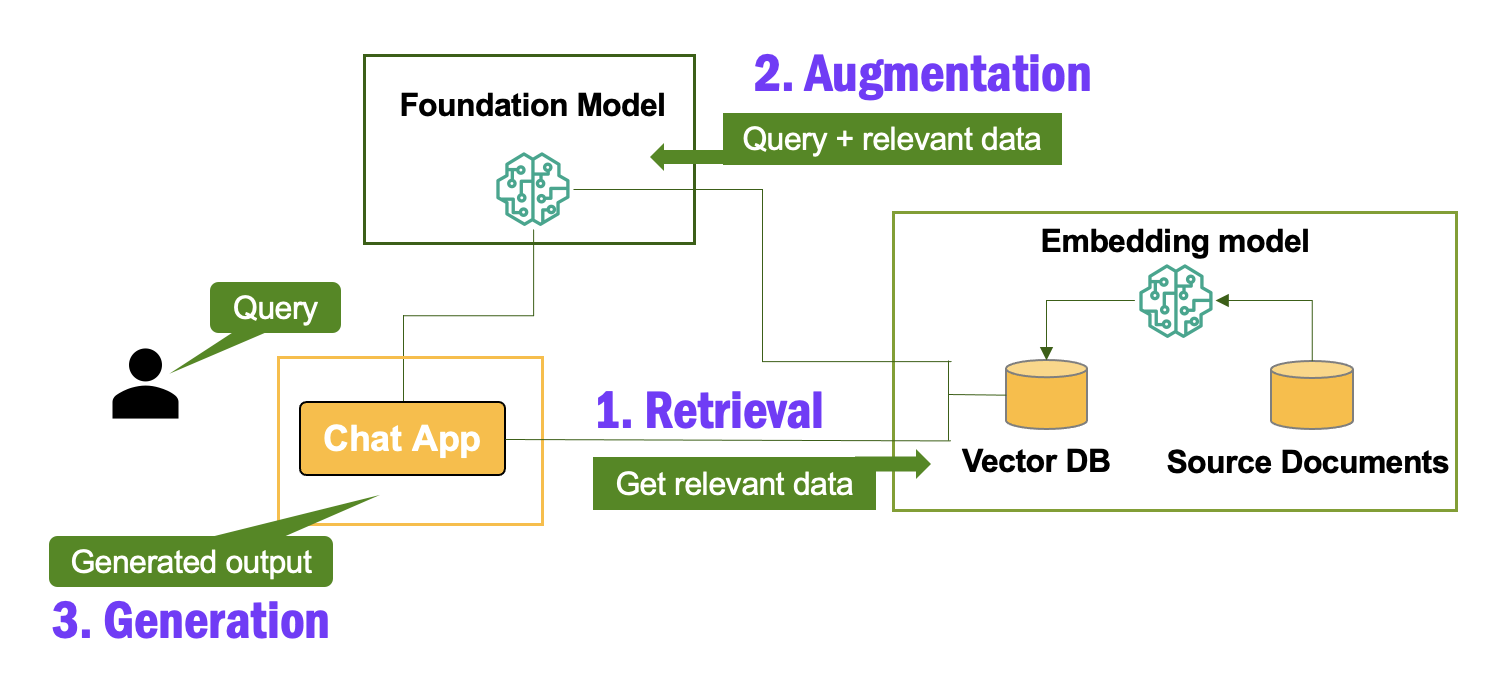
Transforming Parsed Data into Machine-Readable Formats

The transformation of parsed mathematical data into machine-readable formats hinges on preserving both spatial and semantic integrity. 

A critical challenge lies in encoding the hierarchical relationships inherent in mathematical expressions, such as nested radicals or superscripts, without losing their contextual meaning. 

This process demands a meticulous approach where every spatial nuance is mapped into structured formats like LaTeX or JSON.

One advanced methodology involves the use of graph-based models, where each mathematical element is represented as a node, and their spatial or logical relationships are encoded as edges. 

This ensures that the structural dependencies, such as the alignment of fractions or the nesting of operators, are faithfully preserved. 

However, this approach is computationally intensive and requires robust algorithms for edge cases, such as ambiguous notations or overlapping symbols.

In practice, the success of this transformation depends on iterative validation. For example, systems like GLAM integrate visual features with metadata to enhance accuracy. 

These techniques enable RAG systems to process complex mathematical content with unparalleled fidelity by bridging the gap between raw parsing and structured representation.

Ensuring Semantic Accuracy in Mathematical Expressions

Semantic accuracy in mathematical expressions hinges on preserving the intricate relationships between symbols, often conveying meaning through spatial positioning. 

A critical technique involves integrating layout analysis with semantic tagging, ensuring that both the geometric and logical structures of formulas are captured. 

This dual-layered approach is essential for maintaining the integrity of nested hierarchies, such as fractions within radicals or superscripts tied to specific variables.

One standout methodology employs graph-based models, where each symbol is treated as a node and its spatial relationships are encoded as edges. 

This framework excels in handling complex expressions, allowing for precise mapping of dependencies. 

However, its effectiveness depends on iterative validation to address edge cases, such as overlapping glyphs or ambiguous notations. 

For instance, root symbols with detached components often require specialized algorithms to avoid misinterpretation.

A comparative analysis reveals that while OCR-based systems struggle with these nuances, hybrid approaches combining graph models with machine learning offer superior adaptability. 

Yet, these systems face challenges in standardizing outputs across diverse document formats, highlighting the need for robust normalization techniques.

Tools like MathML-based parsers have emerged to bridge theory and practice, enabling seamless conversion of parsed data into machine-readable formats. 

This synthesis of spatial precision and semantic depth enhances RAG system performance and sets a foundation for scalable, accurate mathematical data retrieval.

Integrating Parsed Content into RAG Pipelines

Integrating parsed mathematical content into RAG pipelines transforms static data into actionable intelligence by bridging the gap between raw extraction and meaningful application. 

This process hinges on converting parsed outputs, such as LaTeX or MathML, into structured formats like JSON, enabling seamless interaction with retrieval and generation components. 

A common misconception is that parsed data can be directly utilized without further refinement. 

However, inconsistencies in font encoding or ambiguous notations often necessitate normalization techniques. 

Tools like Neo4j, which leverage graph-based representations, excel in preserving the semantic relationships between symbols, ensuring that nested structures like matrices or radicals are accurately interpreted.

By embedding this structured data into RAG workflows, systems achieve higher accuracy and scalability, unlocking advanced applications such as automated theorem proving and domain-specific question answering.

Enhancing AI Models with Structured Mathematical Data

Structured mathematical data is a cornerstone for refining AI models, particularly in Retrieval-Augmented Generation (RAG) systems. 

A critical yet often overlooked aspect is graph-based representations' role in preserving mathematical expressions' semantic and spatial integrity. 

These models map symbols as nodes and their relationships as edges, ensuring that nested structures like radicals or matrices are accurately encoded.

This approach matters because even minor inconsistencies—such as misaligned superscripts—can disrupt downstream reasoning processes. 

By leveraging graph-based methodologies, AI systems gain a robust framework for interpreting complex formulas, enabling precise query responses and advanced computations. 

However, this technique demands significant computational resources and careful calibration to handle edge cases, such as ambiguous notations or overlapping glyphs.

A comparative analysis reveals that while traditional OCR systems struggle with these nuances, graph-based models maintain structural fidelity. 

Yet, their effectiveness depends on iterative validation and normalization techniques to standardize outputs across diverse document formats.

Organizations like Neo4j have demonstrated improved retrieval accuracy and scalability by embedding these structured outputs into RAG pipelines. This synthesis of spatial precision and semantic depth enhances AI performance and sets a foundation for future innovations in automated reasoning.

Challenges and Solutions in Mathematical PDF Parsing

Parsing mathematical PDFs demands precision, as even minor errors in spatial interpretation can cascade into systemic inaccuracies. 

A key challenge lies in decoding multi-line equations, where misaligned baselines or fragmented glyphs disrupt semantic coherence. 

Another obstacle is the inconsistency in font encoding across PDFs, which complicates symbol recognition. 

Adaptive algorithms, such as those leveraging stochastic context-free grammars, have shown promise in normalizing these variations. 

These methods dynamically adjust to diverse document structures, ensuring robust parsing even in edge cases.

A counterintuitive insight is that simpler OCR systems often outperform advanced models in recognizing isolated symbols but fail in reconstructing nested hierarchies. 

This underscores the importance of integrating graph-based models, which map spatial relationships as nodes and edges, preserving the formula’s structural integrity for downstream RAG applications.

Handling Complex Equations and Multi-line Formulas

Decoding multi-line formulas in PDFs requires more than symbol recognition; it demands a nuanced understanding of spatial relationships and baseline shifts. 

Even minor misalignments can disrupt the semantic flow when equations span multiple lines, leading to misinterpretation. This complexity underscores the need for advanced parsing techniques that integrate spatial analysis with structural logic.

A standout methodology combines layout-based detection with machine learning models trained on multi-line equation datasets.

Layout analysis identifies line breaks, alignment patterns, and spacing irregularities, while machine learning adapts dynamically to diverse formatting styles. 

This hybrid approach excels in preserving the hierarchical structure of equations, ensuring that nested components like fractions or summations remain intact.

Comparatively, traditional OCR systems often falter in these scenarios, treating each line as an independent entity, ignoring cross-line dependencies. 

In contrast, graph-based models map symbols and their relationships across lines, offering a more cohesive representation.

However, these models require extensive computational resources and careful calibration to handle edge cases, such as overlapping symbols or ambiguous notations.

A practical example is the integration of these techniques into academic publishing workflows, where precise formula parsing ensures consistency in digital archives. 

This approach enhances retrieval accuracy and sets a benchmark for handling complex mathematical content in AI-driven systems.

Overcoming Handwritten Mathematics Recognition

Handwritten mathematics recognition presents a unique challenge due to the variability in writing styles, symbol shapes, and spatial arrangements. 

A particularly effective approach involves leveraging convolutional neural networks (CNNs) trained on diverse datasets that capture these variations. 

Unlike traditional OCR, which struggles with irregularities, CNNs excel at identifying patterns and contextual relationships within handwritten symbols.

One critical component of this process is attention mechanisms within neural networks. 

These mechanisms dynamically focus on specific regions of an input image, enabling the model to prioritize key features like symbol alignment or overlapping strokes.

However, challenges persist, particularly with ambiguous symbols or inconsistent baselines. 

To address this, hybrid systems combining CNNs with rule-based post-processing have emerged. 

These systems refine outputs by applying domain-specific rules, ensuring that recognized symbols adhere to mathematical conventions. This dual-layered approach enhances accuracy and preserves the semantic integrity of equations.

By integrating these advanced techniques, practitioners can transform handwritten mathematics into structured, machine-readable formats, unlocking new possibilities for Retrieval-Augmented Generation systems and beyond.

FAQ

Conclusion

Parsing mathematical PDFs is essential for accurate and scalable Retrieval-Augmented Generation applications. 

By focusing on spatial structure, semantic accuracy, and structured output formats, systems can extract reliable data from complex formulas. These techniques ensure that RAG models respond with precision across academic, legal, and technical domains.